BK-Trees

2012-01-17

A BK-Tree is a really cool data structure for building a “dictionary” of similar words. It can be used to guess that you meant “cat” when you wrote “cta”. It works by building a tree with words from a dictionary by using the first word as a root node and then attaching subsequent words with a branch of length d(root_word, new_word) where d is a function for finding the “distance” between two words. This is usually the Levenshtein_ distance, i.e. the minimum number of edits needed to transform one string into the other.

If the branch is “taken”, i.e. there is already another word connected along a branch of length d(root_word, new_word), the insert operation is done on this word instead. That is the whole algorithm for constructing the BK-tree.

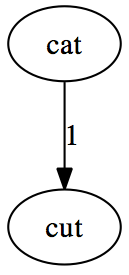
So if we have the following list of words: ["cat", "cut", "hat", "man", "hit"], we will start by creating a “cat” node with no children. To add “cut” we calculate the Levensteinh distance to be one and insert it under the “cat” node.

1) Cut is inserted under cat with a branch of length one

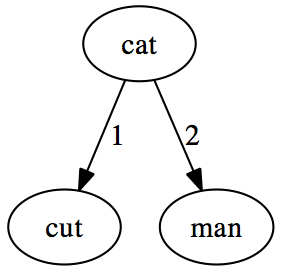
2) The Levensteinh distance between “cat” and “man” is two, so “man” is connected with a branch of length two

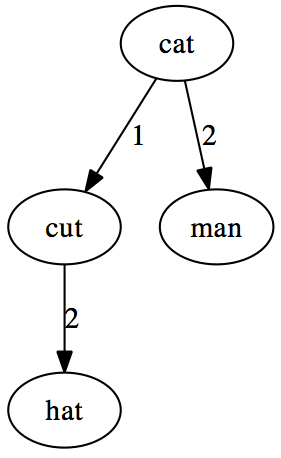
3) d(“hat”,“cat”) = 1, so the insertion operation is done on the “cut” node, and “hat” is connected to “cut” with a branch of length two (d(“cut”,“hat”)=2)

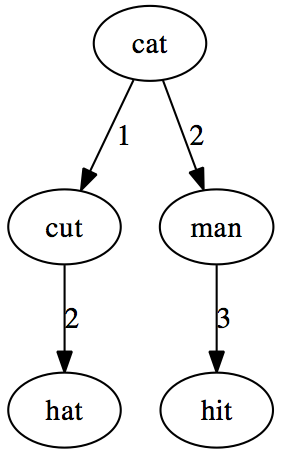
4) d(“cat”,“man”) = 2, so the insertion operation is done on the “man” node, and “hit” is connected to “man” with a branch of length three (d(“man”,“hit”)=3)

The query algorithm is also simple: We find the distance d from the query word to the root node. If this is less than the maximum distance we allow, n, we include this word in the result. We then find all the child nodes connected by branches of length (d-n) ≤ l ≤ (d+n) and recursively query these nodes and add to the result. The result is a list of words satisfying d(query_word, word) ≤ n.

The following code is a Haskell implementation of BK-Trees.

import qualified Data.Map as M
import Control.Applicative
import Data.Maybe (mapMaybe)

-- A BK-Tree is has a root word and more trees connected to it with branches of
-- lengths equal to the Levenshtein distance between their root words (i.e. an
-- n-ary tree).
data BKTree s = BKTree s (M.Map Int (BKTree s)) | Empty deriving (Show)

-- Inserting a word is done by inserting it along a branch of lenght
-- [Levenshtein distance] between the word to be inserted and the root. If
-- there is a child node there, change focus to that child and continue the
-- operation.
insertWord :: BKTree String -> String -> BKTree String
insertWord Empty  newWord               = BKTree newWord M.empty
insertWord (BKTree rootWord ts) newWord =
  case M.lookup d ts of
       Nothing -> BKTree rootWord (M.insert d (BKTree newWord M.empty) ts)
       Just c  -> BKTree rootWord (M.adjust (flip insertWord $ newWord) d ts)
    where d = levenshtein rootWord newWord

-- Querying the tree consists of checking the Levenshtein distance for the
-- current node, then recursively checking all child nodes connected with a
-- branch of length [(d-n),(d+n)]
query :: Int -> String -> BKTree String -> [String]
query n queryWord (BKTree rootWord ts) = if d <= n
                                            then rootWord:ms
                                            else ms
  where -- Levenshtein distance from query word to this node's word
        d  = levenshtein rootWord queryWord
        -- find child nodes in the range [(d-n),(d+n)] ...
        cs = mapMaybe (`M.lookup` ts) [(d-n)..(d+n)]
        -- ... recursively query these child nodes and concatenate the results
        ms = concatMap (query n queryWord) cs

-- Levenshtein distance calculation function taken from
-- en.wikibooks.org/wiki/Algorithm_Implementation/Strings/Levenshtein_distance
levenshtein :: (Eq t) => [t] -> [t] -> Int
levenshtein sa sb = last $ foldl transform [0..length sa] sb
    where transform xs@(x:xs') c = scanl compute (x+1) (zip3 sa xs xs')
              where compute z (c', x, y) = minimum [y+1, z+1, x + fromEnum (c' /= c)]

ask :: BKTree String -> IO ()
ask bk_tree = do
      putStrLn "Enter query word: "
      queryWord <- getLine
      putStrLn "Enter max distance: "
      dist <- read <$> getLine
      print $ query dist queryWord bk_tree
      ask bk_tree

main :: IO ()
main = do
      -- read dictionary file, skipping comments
      dic <- (filter (not . comment) . lines) <$> readFile "dictionary.txt"

      -- build BK-Tree
      let bk_tree = foldl (insertWord) Empty dic

      ask bk_tree
  where comment []      = True
        comment ('#':_) = True
        comment _       = False

It even works! Here are a few examples where I used a dictionary of ~5800 words:

λ> query 1 "thie" bk_tree
["tie","the","this","thief"]
λ> query 1 "catt" bk_tree
["cat","cart"]

Erlend Hamberg

BK-Trees