Sometimes you stumble over some cool things you really wish you could use right away – like the Prüfer sequence. The Prüfer sequence is a way of uniquely representing trees of n nodes with a sequence of n-2 node labels. The tree shown below, which has six nodes can thus be represented by a string of four labels, namely “3334”.

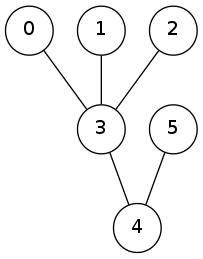
To come up with the Prüfer sequence for the tree you first have to come up with an order for the node labels. For the tree above this is simply 0, 1, 2, …. You then start with the “smallest” label, remove it and add the node it is connected to to the sequence. Here, that would be to remove node 0 and add 3 to the sequence. The next nodes would be node 1 and 2, which are also connected to node 3, yielding the sequence “333” after three steps. You would then remove node 3 and add 4 to the sequence. When only two nodes are left you stop. The final result is thus “3334”.

To go from a Prüfer sequence to a tree you first find the degree of each node, this is simply done by counting its occurrences in the sequence and add one, meaning that node 0 has degree 0+1=1, while node 3 has degree 3+1=4. You can the do the reverse of the encoding process: for each node in the sequence, add an edge from it to the first node with degree 1 and reduce both nodes’ degree. This is done until you have only two nodes left which should be connected.

Python code for decoding a Prüfer sequence into an array of node pairs (connection):

def prufer_to_tree(a):
    tree = []
    T = range(0, len(a)+2)

    # the degree of each node is how many times it appears
    # in the sequence
    deg = [1]*len(T)
    for i in a: deg[i] += 1

    # for each node label i in a, find the first node j with degree 1 and add
    # the edge (j, i) to the tree
    for i in a:
        for j in T:
            if deg[j] == 1:
                tree.append((i,j))
                # decrement the degrees of i and j
                deg[i] -= 1
                deg[j] -= 1
                break

    last = [x for x in T if deg[x] == 1]
    tree.append((last[0],last[1]))

    return tree